Рівняння, що містять змінну під знаком модуля

 При розв’язуванні рівнянь, що містять змінну під знаком модуля, найчастіше застосовують такі методи, як:

a) розкриття модуля за визначенням;

b) метод інтервалів.

За визначенням модуля: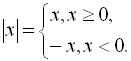  

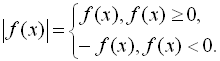
Відзначимо такі властивості модуля, які нерідко використовуються на практиці:       

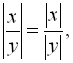
Для найпростіших рівнянь з модулем слід пам’ятати, що рівняння  рівносильне сукупності рівнянь 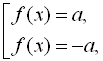 якщо . Якщо ж , то рівняння  розв’язків не має.

Метод інтервалів (проміжків) при розв’язуванні рівнянь з модулями

 

Даний метод полягає в тому, що:

1) вирази, які стоять під знаком модуля, прирівнюються до нуля;

2) отримані значення відкладаються на числовій прямій, яка при цьому розбивається на інтервали (проміжки), в кожному з яких свій знак підмодулевого виразу;

3) розв’язуються отримані рівняння в кожному з інтервалів.

На практиці метод інтервалів зазвичай застосовується тоді, коли рівняння містить декілька модулів.

Розглянемо застосування методу інтервалів на прикладах.

Приклад 18. Розв’язати рівняння .

Розв’язання

1-й спосіб розв’язування:

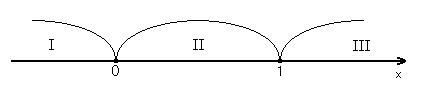
; . Наносимо на числову пряму точки  і . Ці точки розбивають числову пряму на три інтервали (проміжки), у кожному з яких свій знак підмодулевого виразу. Для зручності можна позначити ці інтервали І, ІІ, ІІІ:

І: ; ІІ: ; ІІІ: .

Для інтервалу І маємо: ; .

     Звідси, дістаємо розв’язання рівняння в І інтервалі: . Однак значення  не належить І інтервалу, тобто  , тому в І інтервалі початкове рівняння  розв'язків не має.

     Для ІІ інтервалу ;   початкове рівняння має вигляд . Оскільки  – це тотожність, то будь-яке   є розв’язком, тобто розв’язком рівняння є весь відрізок  .

     Для ІІІ інтервалу ;   початкове рівняння має вигляд: . Оскільки  , то в ІІІ інтервалі початкове рівняння розв’язків не має.